Tree
Pythagorean_tree.md

Probably the Pythagorean theorem is the most memorable theorem from the school geometry course. a2 + b2 = c2 - easy to remember, easy to apply. As they say in Russia, Pythagorean trousers are equal in all directions.
It sounds rhyming with us. Pythagorean pants we call the figure that was used by Pythagoras to prove his theorem (Fig. 1). The theorem itself is a special case of the cosine theorem. This is my favorite theorem, because it is the first theorem of which I have deduced myself.
This kind of figure led one clever man in the 20th century to create an intricate pattern that we now know as the Pythagorean tree. The Pythagorean tree is not a fractal in the meaning of Mandelbrot, since its topological and Hausdorff dimension is 2. However, according to the method of construction and appearance, it is quite a fractal, so we will consider it as such.
What attracts me most about it is that firstly it is a complete binary tree, and as I have already written binary trees are very cool, and secondly there are several ways to build it. I have tried to provide all possible settings for the user.
ATTENTION BE CAREFUL, DRAWING A TREE WITH A LARGE ITERATIONS NUMBER MAY CAUSE THE PAGE TO HANG.The method of drawing
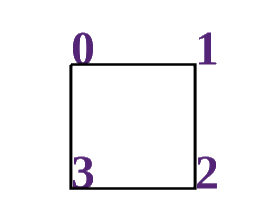
We will have two lists, in the code they are called nodes and leaves. Leaves are drawn and moved to the node list. Each element in the node list spawns two leaves, which are put into the list. This allows us not to keep the entire list of squares in memory (but only half, because each iteration doubles the number of elements). The first square is drawn as a regular square. I hope you can handle it yourself. The main thing is to number the vertices in the correct order (Fig. 2).
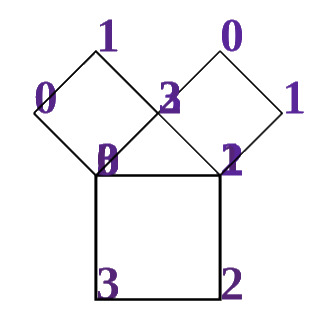
(Fig. 3)
It is entered into the list of leaves. It is drawn and moved to the list of nodes. Then two new squares are built on its basis as follows. The points P0 and P1 are taken. At the middle of the segment between these two points the point PC is taken. Then the point 1 is rotated around the point PC by double angle. Let's call this point T. The segments P0-T and P1-T form the bases for the new squares. Calculate the lengths of the segments. Let us call them LDV and RDV. Now we need to continue the left segment to the right by RDV length and the right segment to the left by LDV length. Then we number the points as in Fig. 3.
Thus repeating this construction for each leaf and transferring the leaf to the list by a node we get amarvelous Pythagorean tree. At this stage the angle of rotation is important to obtain the point T. Technically, it is one of the angles of a right triangle (obviously not the right angle). The other angle is equal to π/2. This parameter affects the slope of the tree, and the size of its right and left subtrees. The size is respectively size*sin(A) for the left and size*cos(A) for the right. Interesting fact! The sums of areas of all squares in each generation are equal! So cool!
Optimization
Since the number of squares doubles with each iteration, computing and drawing the tree can become adrudgery. In the last version I used Pixi.JS and their geometry triangulation, but it was too long, although it gave results in vector graphics. This time I decided to refuse any third party libraries except Next.Js, so I decided to work with a simple Canvas 2d. The first optimization I've already described is the use of two lists so that I don't have to store already drawn squares. This gave an excellent performance gain due to faster work with lists and reduced load on the garbage collector. But it is not enough! If you write data-heavy web applications, typed arrays are your best friends. What's the point of them? Because they are not linked lists like arrays in JS, but contiguous chunks in memory. Access by index is done in O(1). Also, iteration is many times faster. But they have a limitation - such arrays are very poorly expandable. You can even say that they are not expandable at all, they have to be copied completely. But in our case it is not a problem, because we know exactly how many squares we will have. Thus, by calculating the size of the array in advance depending on the number of iterations we get access to any square by index for O(1), iteration for O(n), and clearing for O(1) (we just set the length value to 0).
We could have come up with many more mathematical optimizations, but it turned out to be rather useless, since the profiler showed that most of the time was spent on rendering the tree. This is a real problem. I tried several approaches to drawing - SVG, drawing + applying the affine setTransformationMatrix(), using rotation + fillRect() (works much faster than filling the path), but still drawing slow. The final solution was to use WebGl since GPU power is perfect for this kind of task.
Settings
- Iterations
- The number of iterations determines how deep the tree gets. The number of squares is 2n - 1 where n is the number of iterations (Don't believe me? Check it yourself!). But be careful, because exponential growth is very fast, and it is 32 times easier to render 10 iterations than 15.
- Angle
- One of the acute angles of triangles. Determines the slope of the tree and the size of the subtrees. Very simple to understand, but a very significant parameter.
- Branch long
- I've written everywhere about squares, but this option changes the rules of the game! Extend your squares into rectangles making the tree taller and more graceful!
- Alternation
- I'm not sure if this is the correct name for this parameter, but so be it. Its essence is that it swaps the angles of the triangles after a generation, thus obtaining a new pattern.
- Wobbling
- As we all know, the wind blows because the trees sway. We should rock this tree too. In fact, there are two parameters here - amplitude and frequency. They set the strength and speed of tilting of each rectangular bar depending on time. This way it looks like the tree is swaying. Beauty!
- Color
- my favorite Kandinsky argued that there is nothing more important than color, and I agree with him. I carried over the old colors. Some of them are just random mathematical operations modulo 232. Others have gradients from uigradients.com.
A little more about color

I never tire of expressing my love for binary trees and the binary number system, so here are a couple more facts that I use in the process of calculating the color of a tree. It turns out that the vertices of binary trees are very convenient to number. This is done as follows - for simplicity, let the first element be number one. The left element is obtained by multiplying the current number by two, and the right element by multiplying the current by two and adding one. Thus, we close the entire space of integers from 1 to 2n where n is the number of iterations. But why is that? You can answer as follows. Let's consider the binary system and obtaining numbers in it. We will receive new numbers by adding 0 or 1 to the end of existing ones.
Here we have 0. At the end of it we can assign 02 or one, getting 002 and 012, respectively. 002 = 010, 012 = 110. Moving on - you can assign 0 or 1 to one, getting 102 = 210 or 112 = 310. From 102 we get 1002=410 and 1012=510. Then I think you understand the meaning. An example in Fig. 4. And vice versa - to find out the parent of a vertex, we need to completely divide its number by 2. This is equivalent to erasing the last digit. To find out the depth of a vertex, just take the base 2 logarithm of its number and round down. Amazing. By arranging the vertices, they can be assigned a color according to a linear gradient, just like the Flare and Witching hour colors do.