Newton's pool
Newton's pool.md

(Fig. 1)
When it comes to fractals many people think of the Mandelbrot set. It is a really intricate thing, and even quite pop, as pop as a mathematical object can be. Every year in the center of our campus we plant a flowerbed in the form of a Mandelbrot set (Fig. 1). It's really amazing in its variety. But I decided to don't draw it. Why is that? Most likely because too much attention has already been paid to the mandelbrot set. There are already a lot of ready explorers and videos like zoom into mandelbrot set 10 hours
on the internet. We're kind of underground here, yeah. So here's another fractal for your attention - Newton's pool.
Newton probably didn't realize he had such a wonderful pool. However, he guessed a lot of other interesting and useful things. In this case, we are interested in Newton's method of finding roots. It is quite simple, you may have even heard of it at school. It is an iterative process of converging to one of the roots of a curve. To do this, we need to know the values of the function at the points and the values of its derivative. The formula for this process is xi+1 = xi - xi/xi'. It's really not difficult. It can even be given the following geometric interpretation - at each step of the iterative process we draw the curve at a point, see its intersection with the X axis and repeat the calculations from this point. In the vicinity of the root, the steps will become extremely small and we will hit one of the roots.
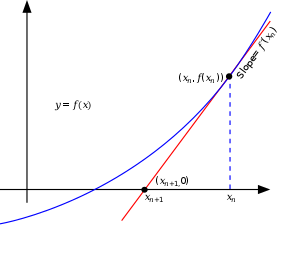
(Fig.2)
But what does this have to do with the topic of fractals and the resulting picture? It takes a little more math. Have you heard anything about complex numbers? If not, read it yourself, this is not an algebra course. If you have an idea of what complex algebra is, it's cool. Let me remind you of a fact that is majestically called The main theorem of algebra. Its essence is that a polynomial of degree N has exactly N roots, possibly complex. Mewover, if it is a polynomial of the form xN - 1, then all its roots are uniformly located on the unit complex circle. Here is another fact - Newton's method also works for complex numbers. See where this is going? We will represent our screen as a complex plane and run Newton's process for each pixel on the screen. After a certain number of iterations, we will see which of the N roots we are closest to and paint the pixel in the color of that root.
The reader sophisticated in industrial fractal production will notice the parallels with the method of constructing a set of Mandelbrot. In general, all algebraic fractals are constructed in the same way. It is also possible to construct Julia's set and Burning Ship and Tricorn.
Implementation details
Compared to the rest of the tops on this site the mandelbrot set is the most uncomplicated to build. I'm using WebGl, and a fragment shader. Who did not know (that silly hee hee hee hee) fragment shader is a program that is executed for each pixel on the screen and as a result of its execution says in what color should be painted pixel. Gosh, it's like shaders are specifically made for algebraic fractals, isn't it? Well, it's really convenient, but there's a little problem. Everything could be much cooler if not for the accuracy of rounding floating point numbers. Precisely because floating-point numbers have a limited (and relatively small) number of symbols after the point when zooming, everything at some point falls into a mess of squares. And then there's that awful monotonous circle in the middle. As a variant to write Big Float directly on GLSL, but so far the hands have not reached. If someone wants to support me in this I will be very glad.